位运算总结,计算机世界里只有 0 和 1
我们知道,目前的计算机最终只认识 0 和 1 这两个数字,我们写的所有代码、指令最终都会变成以 0 和 1 组成的编码执行的,而这样的编码就叫做二进制。
至于为什么是 0 和 1 呢?我简单、非官方地解释一下,因为计算机是由无数个逻辑电路组成的,而电路的逻辑只有 0 和 1 两个状态,0 和 1 并不是简单数字意义上的 0 和 1,它们表示两种不同的状态,0 表示低电平,1 表示高电平。要控制电路来表达某种意思,就只能控制不同电路的不同状态即根据 0 和 1 的有限位数和组合来表达。

因此像我这些从事计算机相关学习或者工作的人就自诩「我的世界里只有 0 和 1」。
而今天我要说的「位运算」,就是直接对这些二进制位进行的一些操作,当然也只是在数值方面。常用的二进制位操作有,~(取反)、^(异或)、>>、<<、&(与)、|(或),在 Java 中还有 >>>,下面是一些简单的规则
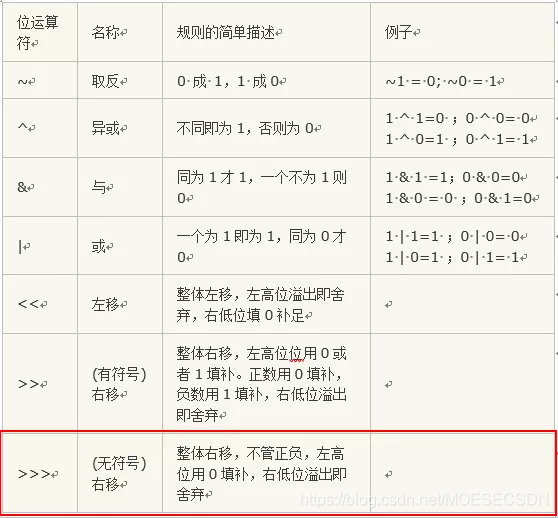
另外补充一下,1 & X = X,0 & X = 0,1 | X = 1,0 | X = X。
最重要的是,在计算机系统中,数值一律用补码来表示(存储)。 因为使用补码可以将符号位和其它位统一处理,同时,减法也可按加法来处理。
其中,如果是我们要人为计算的话(一些面试题,很恶心),碰到负数一定要一万个小心,负数在内存中存储的是它的补码,而它是原码取反加 1 而不是像正数那样,补码和原码一样,另外取反操作也需要特别小心。
~(取反)
0 和 1 全部取反,0 变为 1,1 变为 0。即 ~ 0 = 1,~ 1 = 0。 一定要特别要注意的是,这里的 0 和 1 是二进制位中的,它是一个位,跟我们常用的十进制中的 0 和 1 区别非常大!
举个例子,顺便说一下正数的取反运算,你或许会清楚怎么回事。你觉得下面的代码会输出什么?
class Test {
public static void main(String[] args) {
System.out.println(~1);
}
}
会是 0 吗?大错特错!千万别以为这是前面说的 ~ 1 = 0,答案是 -2

为什么是 -2 呢?
代码里的 1 跟前面规则表格中的 1 区别很大,表格中的 1 是具体到某一位,真正的位操作,而代码里 1 是十进制中的 1,它是 int 类型,在 Java 中,它要用 4 个字节即 32 位来表示,即

那它取反怎么成 -2 了呢?
首先它是正数,它的补码和原码是一样的,也就是 00000000 00000000 00000000 00000001, 特别提醒的是,上面的是 1 的补码,取反之后是 11111111 11111111 11111111 11111110
注意最高位,也就是我们说的符号位,它也会被取反,0 变 1,竟成了负数!同时一定要知道它是补码,要转换成原码的话,先 -1 再取反,因为负数的补码是由原码取反后再 +1,现在是逆过程。

注意在这次取反过程中,符号位是不用取反的,但前面 ~ 取反操作是要取反的,这也是我们很容易错的地方。
再来看看负数 -5 的 ~ 取反操作
class Test {
public static void main(String[] args) {
System.out.println(~-5);
}
}
你可以先动手试试,看看结果是不是 4
 为了方便,我这里就不再以 32 位来做演示,而是只用 8 位,后面有些例子也是如此
为了方便,我这里就不再以 32 位来做演示,而是只用 8 位,后面有些例子也是如此
小结,取反操作是不管符号位的,总之都取反,0 变 1,1 变 0,而在原码和补码间转换时,虽然也有个取反过程,但是符号位是不变的,这也是我们经常会混淆的,是坑。
另外,对所有位操作,实际上都是对它的补码操作,这个适用于任何位操作。对于正数,巧就巧在补码和原码一样,而负数的补码是原码的取反加 1,所以我们也会混淆。
| 与、& 或
对于 ^ 异或运算我在这里就不多说了。就说说我在 | 或运算的小结,大家也可以类推到 & 与运算,然后,再说说 Java 中 >> 和 >>> ,就结束。 码字好累,原创不易,多多点赞支持,谢谢。
先给个小题,16 | 15 = ? 我先不直接揭晓,一起来看看计算过程,还是以 8 位来做演示
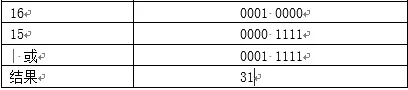
最终结果是 31,不知大家有没有觉得蹊跷,16 | 15 = 31 = 16 + 15,在这里,| 或运算相当于加法运算。
其实还可以看看其他例子,32 | 9 = 41 = 32 + 9

为什么会这样呢?因为 1 | X = 1,0 | X = X ,我们再认真看位运算的过程

我们以第一个加数为基数,末尾除了右起第 6 位,都是 0 ,而第二个加数又小于它,一经过 | 或运算, 0 | X = X ,其实也是将两位数加一起。
所以这里有个小结论,2^N 与一个小于它的数做 | 或运算,其实就是它们两个数之和。知道这个结论,我们以后做题时运算效率就更高一些。就像数字转 IP 的算法就把这个用到极致,它还结合 << 。
public long ipToLong(String ipStr) {
long result = 0;
String[] ipAddressInArray = ipStr.split("\\.");
for (int i = 3; i >= 0; i--) {
long ip = Long.parseLong(ipAddressInArray[3 - i]);
// 等同 A * 256^3 + B * 256^2 + C * 256^1 + D * 256^0,运用位移、或 位运算更高效
result |= ip << (i * 8);
}
return result;
}
更深层次的,在非负两数或运算中,只要两数换成二进制数时,对应的位不是 1 | 1,或运算结果都与加法运算结果一致,我称它为或运算中的非双一现象。
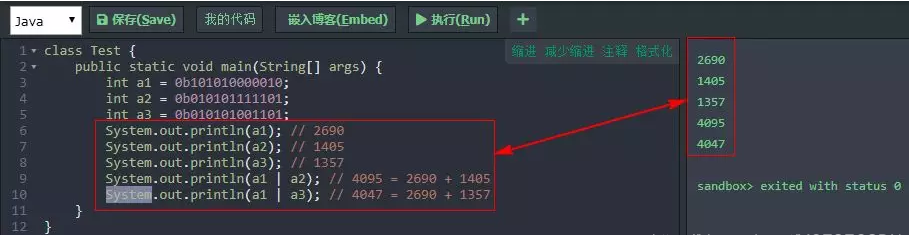
上面的代码就可以很好的诠释,其中 0b 表示二进制数的写法,就好像 0x 表示十六进制一样道理,数值我是随便给的,不是我故意,大家回去可以试试。通常我们会感觉没什么卵用,还不如前面的小结论来得实在点,其实不然,如果知道这些现象且用得非常 6,在加密、算法效率方面用处是非常大的,我就因为欠缺这个而丢失一份很好的工作。
位移
先解释符号及运算规则,>>,带符号右移,正数右移高位补 0,负数右移高位补 1;
4 >> 1 = 2

-4 >> 1 = -2

无符号右移。无论是正数还是负数,高位通通补 0 。
4 >>> 1 = 2

-4 >>> 1 = 2147483646

代码运行结果验证
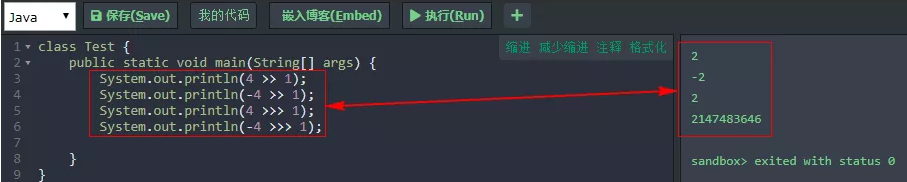
小结一下,对于正数而言,>> 和 >>> 没区别。对于负数,>> 将二进制高位用 1 补上,而 >>> 将二进制高位用 0 补上,区别就很大。
另外,位运算可以帮我们高效地完成很多事情,例如求平均数、判断奇偶、不借助第三方交换两个数 ……,简单了解后,我的世界观都重造了,计算机的世界里好神奇,有兴趣可以查阅相关博客和书籍。